How to Add Decimals: Simple Strategies & Tips

I have recently been introducing my daughter (4th grade) to decimals. We began by understanding what decimals are and what they represent (and how they relate to fractions). We also spent a great deal of time understanding decimal place value and relating decimals to money (because this is an already familiar skill). With this solid foundation in place, we moved to decimal operations, beginning with how to add decimals. The great thing is, once a foundation of decimal place value is there and an understanding of adding money, adding decimals comes easily.

*Please Note: This post contains affiliate links which support the work of this site. Read our full disclosure here.*

Adding Decimals: Begin with Visual Models

Long before we sat down to use the formal algorithm (lining up the decimals correctly and then adding with regrouping), we represented decimals with grids, number lines and money.

For example, we represented decimals using a hundred grid (and base ten blocks) so she could visualize the tenths and hundredths as being less than one whole or part of the whole.

We also spent time relating tenths to fractions and mixed numbers. This allowed her to understand how decimals relate to whole numbers and we then practiced placing numbers on a number line to order and compare them.

We also used place value charts and pictures to show how the decimal parts relate to the whole number parts.

For example, if we have 12 tenths, we can then see that 10 tenths is equal to one whole. Therefore 12 tenths is equal to 1.2 or 1 and 2/10.

This builds a foundation for adding decimals that is not dependent on rules or formulas or algorithms.

So by the time we got to adding decimals to two and three decimal places with regrouping, I never actually taught her ‘how to do it,’ she simply used her knowledge of place value to solve problems herself.

How to Add Decimals Using Place Value:

Understanding decimal place value in our base ten system is essential for knowing how to add decimals.

For example, let’s say you want to add 0.43 + 0.05.

Again, understanding place value helps us to recognize right away that the tenths don’t change because we are adding 0 tenths to the 4 tenths.

Therefore, all we have to worry about are the 3 hundredths and 5 hundredths, which equals 8 hundredths when you add them together.

This makes the final answer 0.48.

Or, let’s say you want to add 0.7 and 0.8.

If you know that 0.7 means 7 tenths and 0.8 means 8 tenths, then you can add them and think of the answer as 15 tenths.

We then know that 10 tenths is equal to one whole. Therefore the answer is 1.5.

And although these are pretty simple and straightforward examples, it lays a foundation for mental math calculation and adding decimals that will strengthen and solidify an understanding of the formal procedure with larger numbers.

Adding Decimals Using Money:

Again, another way to engage kids as they learn how to add decimals is to relate it to something they already know and that interests them: money.

When kids can think of decimals as money, whole numbers represent dollars, tenths and hundredths represent pennies and dimes, it’s less intimidating.

Kids in fourth or fifth grade are likely fairly competent at adding up their loose change or money they received for their last birthday.

So I would encourage you to challenge them with money related problems such as this adding and subtracting decimals lesson before you actually teach them strategies or procedures for how to add decimals.

They will likely pull from their prior knowledge and come up with their own strategies for adding or subtracting decimals without formally being taught.

I would also encourage you to let them use play money (or actual money) to work out problems, again so that they can visualize the decimals.

So for instance, if they are adding 6.78 + 3.43, let them think of this as $6.78 + $3.43 and represent them with play money to add.

This will help them to see that the 0.78 + 0.43 creates another whole number, with some left over.

Again, this helps them to connect what’s happening to the formal algorithm or procedure down the road.

How to Add Decimals: Formal Algorithm

Finally, after kid are familiar and comfortable with representing decimals, understand decimal place value, and can do simple decimal addition mentally, then they can move toward the formal procedure.

This is helpful for kids to know because it will reinforce the procedure with integers (it’s the same basic idea) and it will make computation faster as the numbers get larger.

Step One:

So to begin, all place values must be lined up. This includes the integer or whole number part and the decimal part.

Therefore, tenths need to line up with tenths, ones line up with ones, etc.

Step Two:

Then you add beginning with the smallest place value. For example, if the numbers go out to the thousandths (3 decimal places) you begin by adding the thousandths.

If the number is greater than 10, you carry the one over to the next place value (meaning 10 thousandths is equal to 1 hundredth, so you would write a 1 in the hundredths column).

Step Three:

You then add each place value until the entire problem is solved, continuing to carry when necessary.

Here’s an example for you to see what I mean if you’re not familiar with this procedure:

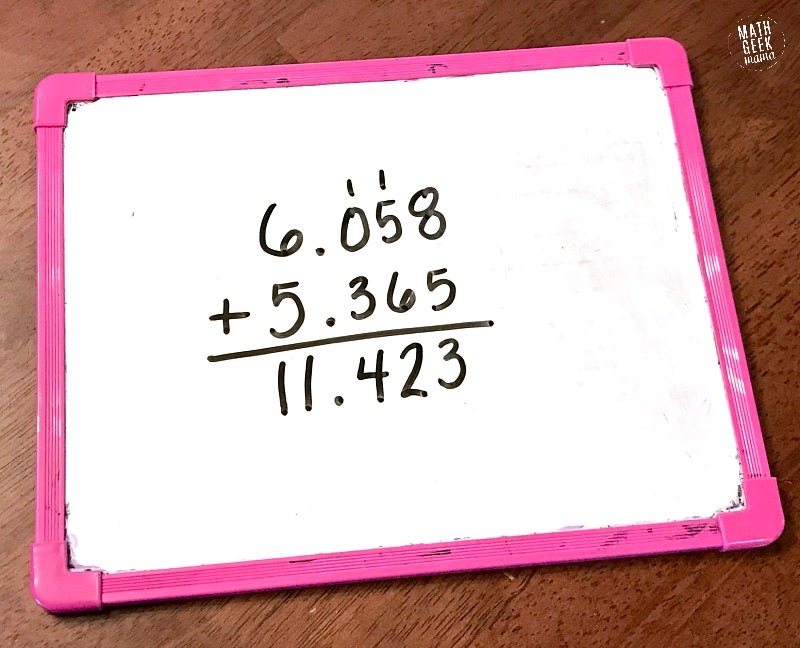
And that’s it!

I hope these tips and strategies are helpful for you, and also know that you can use the same visuals and strategies when subtracting decimals.

Want ready to use resources to help kids visualize decimals? Try my complete add & subtract decimals collection! To see what’s included, you can learn more about it here.