Deepening Fraction Sense with Fractions Area Models

As we continue our series on developing fraction sense, hopefully by now you are feeling a little more confident and equipped. Learning about fractions doesn’t have to be scary, and it doesn’t have to mean hours of pencil and paper computations. Instead, the focus should be on deep understanding, using concrete, visual models. Today, I want to share a powerful visual, which students can use to compare, add, subtract, multiply and divide fractions: area models.

*Please Note: This post contains affiliate links which help support the work of this site. Read our full disclosure here.*

Creating Area Models of Fractions

An area model is a great visual tool because it can be used to make sense of virtually any fraction problem.

It allows kids to see the fraction. This is an important component of developing fraction sense.

But what does that mean? What does an area model look like?

An area model represents a fraction as a rectangle, divided into equal parts. An easy way to do this is to use graph paper.

For example, here’s an area model of the fraction 3/5:

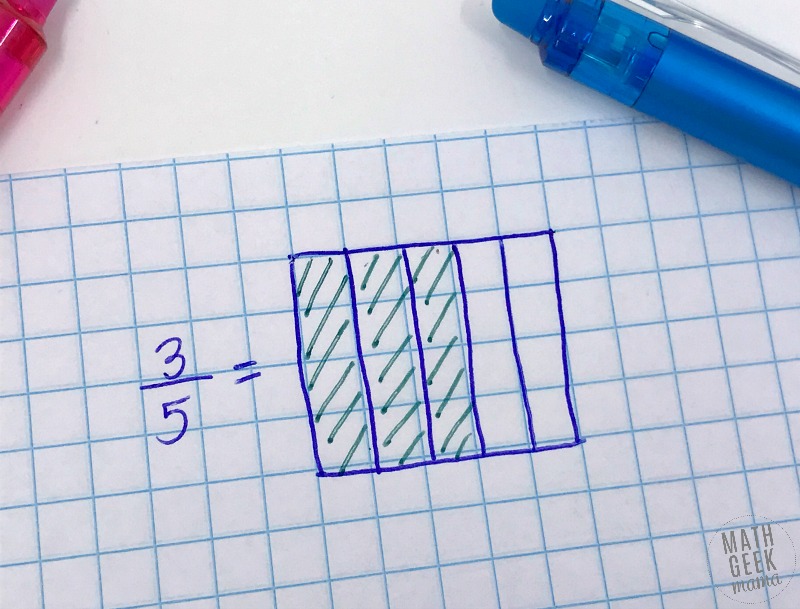
How is this helpful? Let’s explore:

Using an Area Model to Compare Fractions with Unlike Denominators

If students are trying to compare or order fractions with unlike denominators, start by drawing an area model for each fraction.

The first is divided equally with vertical lines, and the second with horizontal lines.

Example: Which is greater, 1/3 or 2/5?

We can’t compare these, because they are not equal sized parts (thirds are not the same as fifths).

In order to compare, we need a common size for the parts (i.e. a common denominator).

This is where our area model comes in.

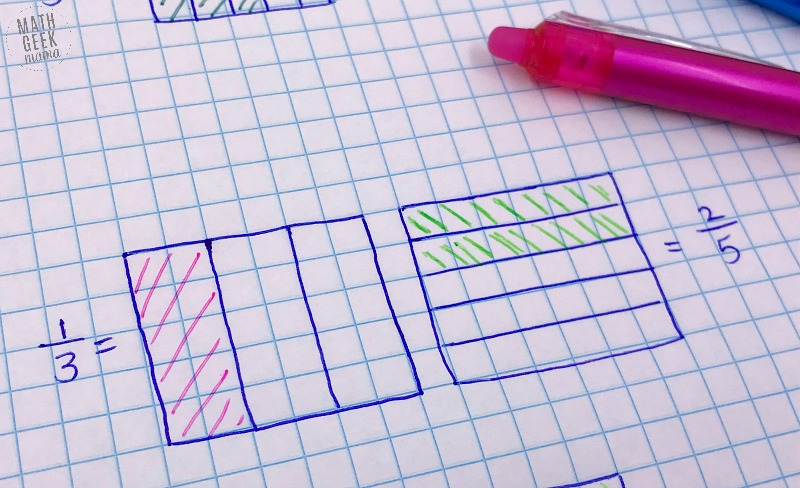
Notice I’ve drawn an area model for each fraction, but one vertically divided and the other horizontally divided. You might be thinking, “Ok, how does that help? I still can’t see which one is bigger…” Hang with me.

I can then overlay the two to get an area divided into smaller pieces.

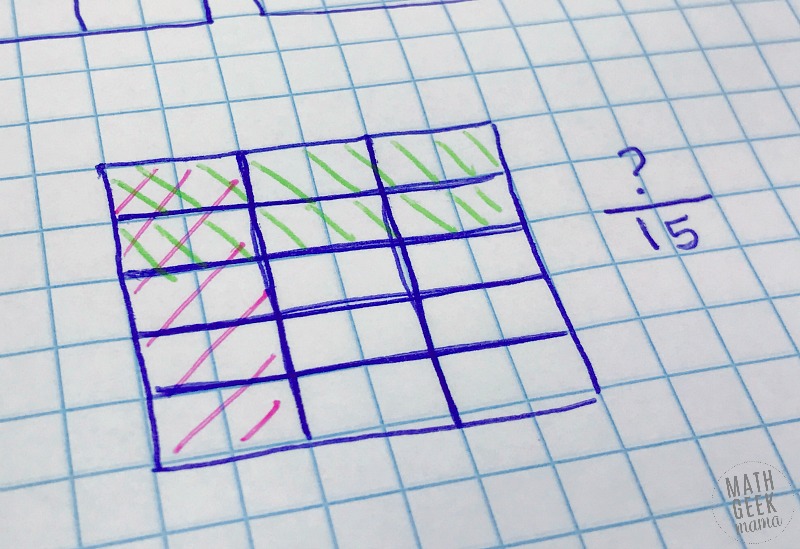
Now my rectangle is divided into 15 parts. I can compare fifteenths.

We can now look at the model and ask, how many fifteenths is 1/3? We count and see there are 5/15 in the colored 1/3 part. Looking then at the 2/5, we see that there are 6/15 in that part.

Now we know that 2/5 > 1/3.

Using an Area Model to Add/Subtract Fractions

Using an area model is also helpful in adding and subtracting fractions with unlike denominators. To start, kids need each fraction to have the same number of parts (again, a “like denominator”).

They can set up area models for each fraction just as we did before to compare.

Then overlay the models to find a new, common “part” and rewrite each fraction.

Once they’ve done this, they can add the fractions easily, because they now have a common denominator.

In the example above, if we were to add them (rather than merely compare them) the final answer would be 11/15.

Using an Area Model to Multiply Fractions

Before beginning to multiply fractions, begin by reviewing whole numbers multiplied by fractions.

For example, 8 x 1/2 is asking, “What is half of 8?” In other words, the answer will only be part of the whole (8), not more. In this case, the answer is 4.

The same is true when you multiply fractions by fractions. If problem says, 1/3 x 1/2, it means, “What is 1/2 of a third?”

In other words, you’re looking for part of the part of the whole. Confused? That’s why visual models are so helpful! Here’s a picture of thirds:

So then multiplying 1/3 x 1/2 means, find 1/2 of 1/3. To do this, we can draw a horizontal line to show 1/2.

But we only want half of 1/3, not the whole thing.

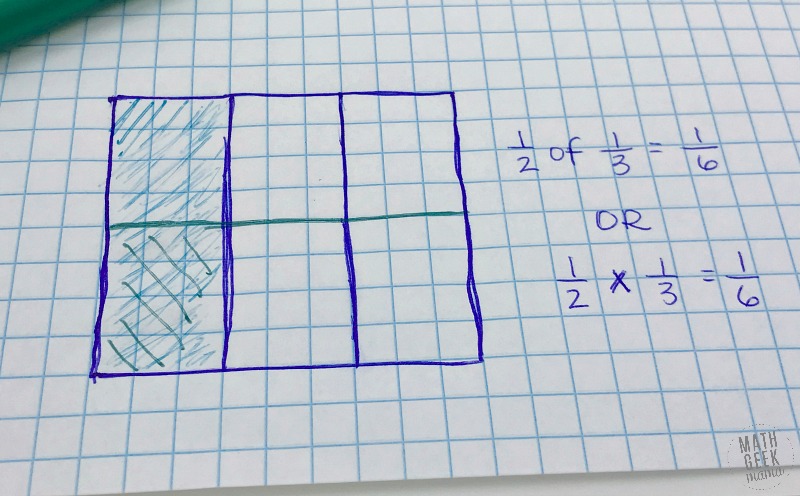
So we see now that the rectangle is divided into 6 equal parts. So half of the shaded third would be represented by 1/6 of the whole.

Therefore, 1/3 x 1/2 = 1/6

This is just a basic introduction to area models, so if this is new to you, I encourage you to go and learn more and practice lots of examples yourself before teaching with area models.

Start by watching videos on YouTube, LearnZillion or Khan Academy, then practice some yourself and with your kiddos!

And be sure to check out the rest of our series on Developing Fraction Sense:

• Understanding the Numerator and Denominator
• Comparing Fractions with Benchmark Fractions
• Understanding Fractions Using Number Lines

And if you want more ideas for hands on fraction fun, check out my ebook: Hands On Fraction Activities! This book includes TONS of lessons using rulers and paper folding (also great visual models to understanding fractions).