Understanding the Angles in Triangles
I love letting kids investigate and explore and see math ideas and patterns for themselves. As an Algebra teacher, this was not always easy to do, but Geometry, on the other hand, really lends itself to being explored. Geometry is the math of lines and points and shapes: solid and three dimensional. So why in the world teach it by having kids right down a set of theorems to memorize? Today I want to share a fun and super simple example involving the angles in triangles. As I’ve shared before, it can be so fun exploring triangle properties! This lesson helps students understand interior and exterior angles in triangles.

*Please Note: This post contains affiliate links which help support the work of this site. Read our full disclosure here.*
This lesson includes two parts, showing students properties of angles that they will need to know in Geometry. These are important, but if you simply tell students they’re true, they will likely forget, and then have no way to figure it out again.
If you let them learn firsthand, however, they can always recreate the situation to figure it out again in the future if they forget.
So I hope you will find this investigation fun and useful!
Materials Needed to Explore Interior and Exterior Angles in Triangles:
- Construction paper
- Scissors
- Student handout (free download, click the link below)
The first lesson is intended to show students that the sum of the interior angles in a triangle (any triangle) is equal to 180 degrees.
That sounds simple enough, and again, you could just tell students this. But I think letting them see it and prove it themselves is more fun (and hopefully more meaningful to them!).
To use the lesson, students start by cutting out multiple triangles from their construction paper.

Encourage them to cut different sizes and types of triangles (acute, obtuse, large, small) so they have a variety.
Then have a discussion about the angle measurements. Do they think the sum of the angles will always be the same? Or will it be greater for larger triangles?
Students will also need to know that a straight line is equal to 180 degrees. If they don’t know this, have them look at their protractor to see a straight line measurement.

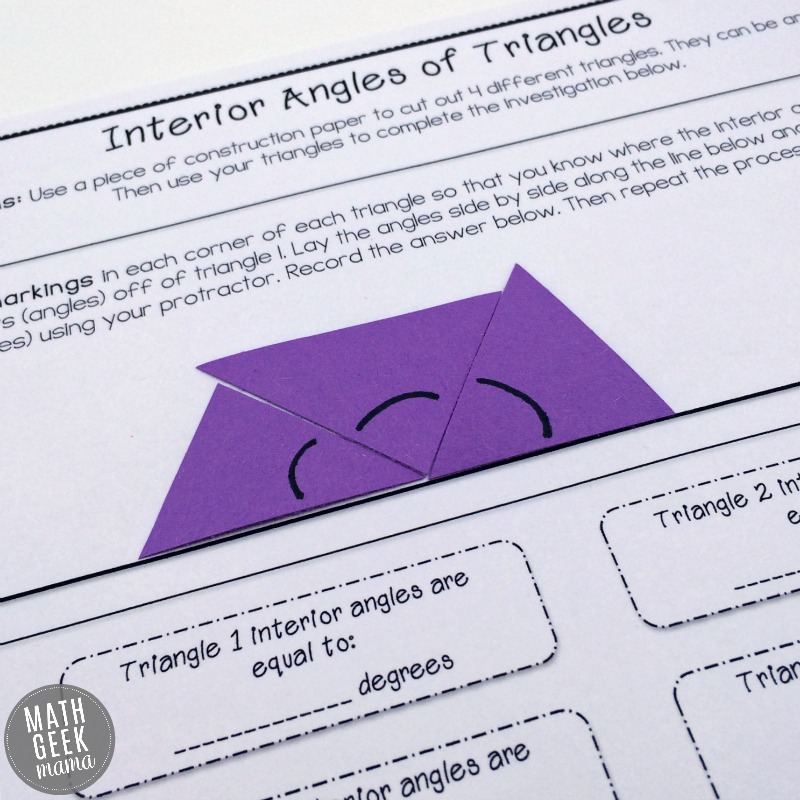
Then students can begin the investigation. The purpose is for them to “cut off” the angles in each triangle and line them up on a straight line to find their sum.
In each case, no matter the triangle, the three angles will fit on the line to equal 180 degrees.

*It is important that students label or mark their interior angles before cutting them off, however, because cutting will form new triangles. If they haven’t marked the original, they will not know which angles they were supposed to be measuring.*
After completing and discussing this first lesson, you can move on to exterior angles.
Understanding Exterior Angles in Triangles:
This lesson will probably require a bit of explanation before you let students begin.
An exterior angle is formed when one of the sides is extended. This creates two angles that are equal to 180 degrees, the adjacent interior and new exterior angle.
The goal of this second lesson is to show students that the sum of the two remaining interior angles (opposite the exterior angle) are equal to the exterior angle.
It is fairly easy to see why this is true:
The sum of the 3 interior angles is equal to 180 degrees, and the sum of the exterior angle and adjacent interior angle is equal to 180 degrees.
Therefore, the difference between 180 and the adjacent interior angle is equal to the two opposite interior angles. (180 – adjacent interior angle = sum of the two interior angles)
Likewise, the difference between 180 and the adjacent interior angle is equal to the exterior angle (because they form a straight line). (180 – adjacent interior angle = exterior angle)
Therefore, the two opposite interior angles and the exterior angle must be equal.
So to help show this to your students, they will cut off the interior angles and compare them to whatever exterior angle they form with their triangle.
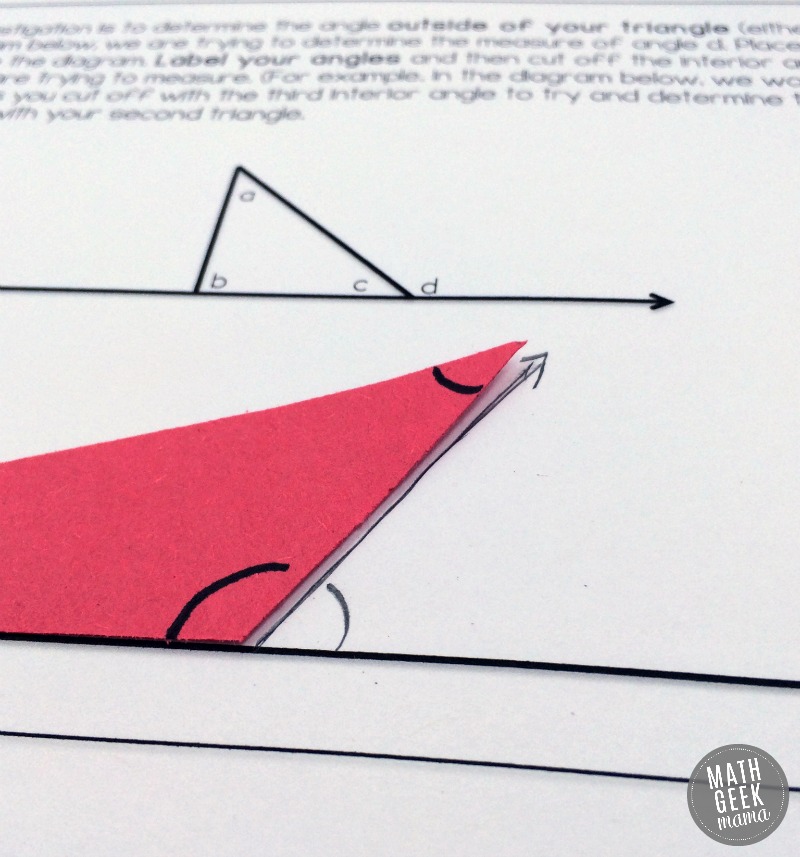
I suggest they trace the side of the triangle that forms an exterior angle to help them see which angles they’re comparing.
Again, they should mark the interior angles, then cut them off to line up with the exterior angle.

They should see, no matter what exterior angle they form, or what their triangle looks like, that the two opposite interior angles are equal to the exterior angle.

I hope I’ve explained this in a way that’s clear. It is really easier to see that it’s true than to explain it in words (I think). Which, obviously, is why I think it should be shown to students as well, especially younger students who are being exposed to angles, angle measures and properties for the first time.
I’ve included some teaching explanations in the download as well, and an answer key for the discussion questions.
Most of all, I hope this guided lesson is a fun and helpful introduction to the interior and exterior angles in triangles, that helps your students understand and make sense of geometry!

{Click HERE to get a copy of the “Interior and Exterior Angles in Triangles” lessons!}
Want more fun, hands-on Geometry ideas? Try one of these FREE lessons!
- Exploring Triangles with The Greedy Triangle
- Understanding Volume of 3D shapes
- Understanding the Surface Area of Prisms and Cylinders
- Exploring 3D shapes with a 3D pen













Are you sure you aren’t a fly on a wall in my home? My fifth grader covered this very thing in math last week! I had a crazy idea to have him cut out triangles, mark the interior angles, cut them off, and then see if they made a straight line. He kept saying “I know it is, Mom.” But I made him prove it anyway. His younger sisters thought it was pretty cool to see him using their glue sticks, too.
Thanks for a great printable & lesson. I’m filing away for a short week to use as a review – and to see if he still “knows it, Mom.” 🙂