Disney Math: Frozen Fractal Snowflake {FREE Printable}
Do you know what a fractal is? I LOVE fractals! Fractals are geometric shapes with self-similar patterns, created by repeating a process over and over again. While there is a wonderful complexity to fractals, there is also a beautiful simplicity that even small children can enjoy! In this next post in my Disney Math series, I’m sharing how I introduced my kids to fractals, based on the movie Frozen. Learn how to make a simple fractal snowflake, then get creative and design your own!

*Please Note: Some of the links in this post are affiliate links and help support the work of this site. Read our full disclosure here.*
Disney Math: Create a Fractal Snowflake
If you’ve never paid much attention to the song, “Let It Go,” you may not have noticed, but there’s a line that she sings that says, “My soul is spiraling in frozen fractals all around.” You see, many patterns in nature have fractal qualities, like plants and trees. So after exploring fractals with your kids, and drawing some, get outside and look for them in the world around you!
The fractal I’m going to share today was described by mathematician Helge Von Koch in 1904, and is known as the Koch Snowflake (or curve, star). Although you could measure for precision, my goal was to simply show my kids the repetitive process and explore patterns, so we didn’t measure. 🙂 For more on this fractal, and more precise measurements, check out this post!
To start, you need to draw an equilateral triangle (or an approximation). This is also a good chance to talk about properties of triangles!

While we did not measure, we did use a ruler (Frozen-themed, of course) to make sure our sides were straight and neat.
The basic process then, is to erase the middle third of each side and draw a point (forming another equilateral triangle).

My daughter was THRILLED to have a reason to pull out her ruler, haha!

Again, we did not measure, I just helped her erase, and then I drew a dot where the point should meet and let her use a ruler to draw the actual lines. After the second iteration, it should look something like this:

I absolutely loved introducing my algebra students to fractals, because they create such beautiful linear patterns! To start, our shape had three sides. Notice, after the second iteration, it now has twelve sides. Why is that?
To continue our process, we now have to erase the middle third of each of the twelve sides and draw a point. Notice what happens to the number of sides our fractal snowflake has!

It might not seem like it, but this snowflake now has 48 sides! Counting them all was somewhat daunting for her, and she was ready to move on and create her own fractal (have I mentioned she’s incredibly artsy and creative?), so she stopped her snowflake there and got busy creating her own design.
My son, however, wanted to see it through! So when he was creating his snowflake, I went around and erased the middle of each of the 48 sides and then let him draw a point. Here’s his snowflake after four iterations:

Pretty cool, huh? Any idea how many sides his snowflake has now? 192. Do you see the pattern? The number of sides is being multiplied by four at every stage in the process!
Here’s mine that I drew as I was helping them and showing them what to do:
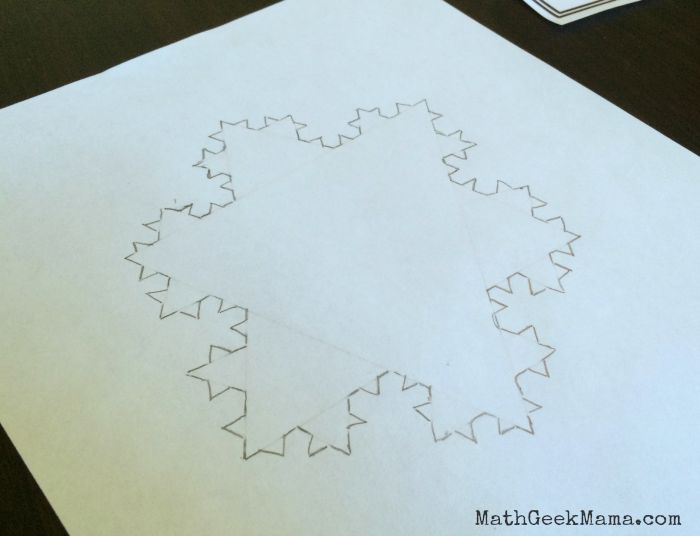
Again, it’s not precise, but it gave them a good picture of the patterns and the new shape that gets created. And even though they are not learning multiplication right now, it was great for them to see and count how quickly the number of sides was growing. We also talked about how after each iteration, the sides were shorter.
When teaching algebra, I would also use this as an example for students to see why having mathematical equations to represent patterns in the real world is important. I was only able to draw this to four iterations. What if I wanted to know how many sides there would be at stage 5? Stage 50? Plugging that into an equation is infinitely faster and easier than drawing or even creating a table of values would be.
Because my daughter loves Frozen, I created this fun little printable for her to use and color, and I printed several because she loves to draw and create and I knew she would want to make more than one snowflake. If you’d like this fractal snowflake page too, just download it below!

{Click HERE to go to my shop and download the Frozen Fractal Snowflake Drawing Page!}
What do you think? Do you like to explore fractals? Ever tried to create your own? Want more resources? Check out this page from The Fractal Foundation and grab their free educator’s guide to learn more and engage your students! Plus, find more advanced math to explore in this wikipedia article.
Want more fun, Disney Math ideas? Don’t miss our Disney World countdown, as well as Building Cinderella’s Castle with pattern blocks!













Oh my! You are so gifted!! You find math in everything AND bring complex concepts down to a young child’s level. Wish I had had you as a teacher! 🙂 Filing this away for this winter when we do a short unit study on snowflakes. Thank you!
Oh you’re so sweet!! I hope you guys enjoy it!! 🙂
Love this! I’ll be using this idea for some winter time math. Thanks so much for sharing!
That’s great! I think we’ll be pulling it out again this winter because my kids loved it! And the other day my daughter saw something and said, “Look mom, that’s like a fractal!” I was so excited that she was observing the patterns and referring back to this lesson!