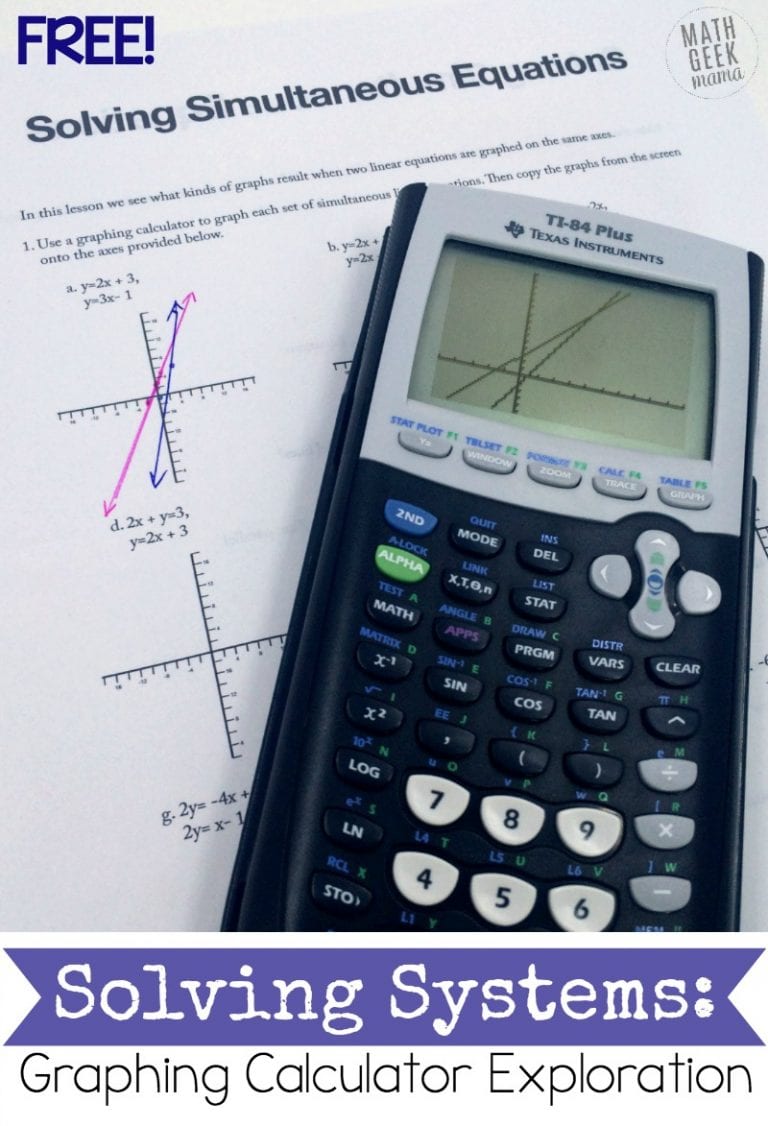
Height of a Building: Indirect Measurement Lesson | Grades 7-8

ByBethany

Looking for a fun way to help your kids practice and understand indirect measurement? This free indirect measurement lesson will get kids outside, applying their math skills to real life.

One of the biggest overarching math concepts in middle school is proportional relationships. We see proportional relationships in real life all the time, and it’s important that students can recognize them, but more than that apply proportions to solve real problems. There are a lot of applications, but one easy way to show students a proportional relationship is through indirect measurement. By creating similar triangles, we can create proportions to find a good estimate of things that are too tall or difficult to measure more precisely. In this lesson, Find the Height of a Building, students will apply their knowledge as they get outside and see it in action.

What is Indirect Measurement?

Indirect measurement means finding an unknown measurement of an object that is difficult to measure directly, with a ruler or measuring stick.

When you cannot directly measure an object, you can use other measurements to indirectly estimate the measurement you’re looking for.

For example, you may not be able to easily measure the height of a tree in your back yard, the height of your house or the height of an office building downtown.

These things are significantly taller than you, so you can’t simply hold up a measuring tape to find the height.

You can, however, use a very clever application of similar triangles to estimate the heights of these objects. This is known as indirect measurement.

Applying Similar Triangles to Indirect Measurement:

What does it mean for two triangles to be similar? Before we can begin our lesson on indirect measurement, we have to understand similar triangles.

Similar triangles have the same shape, but are different sizes. This means all corresponding angles are equal, but corresponding side lengths are not equal. This is what makes similar triangles different from congruent triangles.

Congruent triangles have equal corresponding angles and equal corresponding sides. So they are the same shape and the same size.

Although similar triangles do not have equal corresponding sides, they have an interesting relationship that we will put to work in our indirect measurement lesson: corresponding sides all have equal ratios. In other words:

Similar triangles have equal corresponding angles and all sides are of equal proportion.

Because we can create a proportion out of the corresponding sides of similar triangles, we can use that proportional relationship to find the measurements of known side lengths.

So how in the world does this relate to finding the height of a building?? Let’s find out.

Finding the Height of a Building: An Indirect Measurement Lesson

To use indirect measurement, we will need two similar triangles.

The fun part of this lesson is that when you step outside on a sunny day, you (and other objects around you) cast a shadow on the ground.

Using your height and your shadow, you can create a right triangle.

The best part? At that moment, everything that is casting a shadow on the ground now has created a similar right triangle to you and your shadow.

Materials Needed:

  • Student handout for each student (grab it free in my shop!)
  • Clipboard
  • Measuring tape for each pair/small group

Overview of the Lesson:

So the basic premise of this lesson is that you can use direct measurement to find the height and shadow length of an object that is easily measurable.

Then, you measure the shadow length of the object that is too difficult to measure directly.

Then you set up a proportion using the two similar triangles to solve for the unknown measurement (in this case, the height of a tall building).

Although the basic idea is pretty straightforward, the lesson includes a few more parts to help guide students and make sure they understand what they’re doing and why it works.

Lesson Steps:

In step one, students will briefly review similar triangles and using proportions.

I recommend reviewing this problem in your classroom and discussing it together before you head outside.

In step two, students will use direct and indirect measurement to find the height of something small and measurable.

The goal of this step is to compare their measurements and begin to think about why precision matters and see how close their estimate is to the actual measurement.

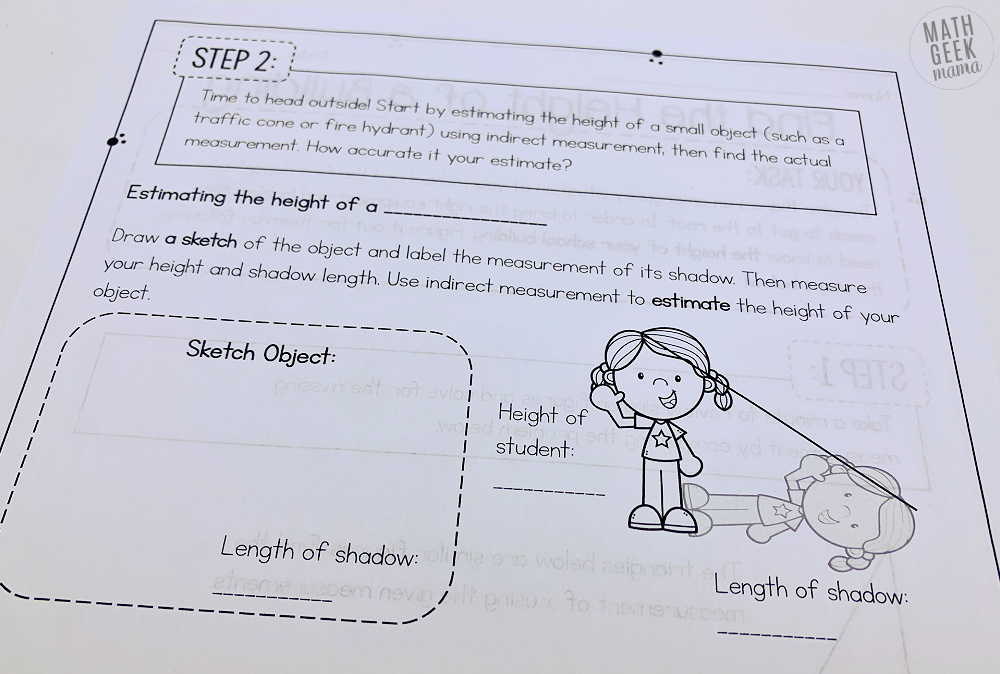
This is also another opportunity to review measuring and creating proportions with similar triangles.

In step three, students will measure the shadow of their school building and once again create a proportion to estimate the height of the building.

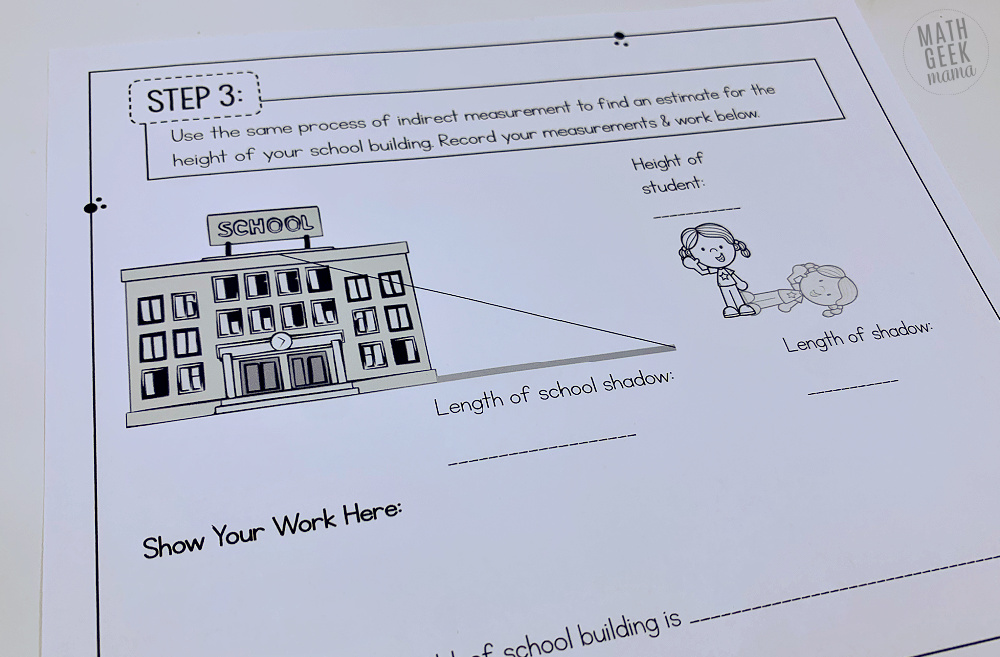
In step four (which you can do back in your classroom), students answer some questions as they reflect on what they did and what they learned.

Indirect Measurement Lesson Wrap-Up:

Once all students have completed the tasks, head back inside to compare and discuss.

When I used this lesson with my 8th grade students, we will in a brand new school building. Lucky for me, I knew the builder and I was able to reach out and get the actual, exact height of our new school building.

We were able to turn this into a little competition, with the group finding the closest estimate to the actual height earning a prize.

Although this is certainly not necessary, it definitely helps to be able to wrap up the lesson by revealing the actual height of the building.

This naturally leads into a discussion of why the estimates were different from each other and also different from the actual.

You can also find the average of all the estimates. Is this closer to the actual? Why?

Lastly, you can discuss other possible applications for indirect measurement.

And once you’re finished, if your students need additional practice with similar triangles, proportions and indirect measurement, you might try this similar triangles classroom scavenger hunt.

It includes 10 problems to post around your room. Students walk around solving them and finding the solutions until they have completed all 10.

It also includes two independent practice worksheets, which you can use for informal assessments or review.

Learn more and grab the Similar Triangles Scavenger Hunt HERE.

If you enjoy this lesson, become a Math Geek Mama+ member and gain access to the entire library of engaging math lessons like this one, hundreds of math games and low-prep practice worksheets for grades 5-8!

Learn more about Math Geek Mama+ right HERE.

Ready to get started? Click the link below to go to my shop and grab this free math lesson!

{Click HERE to go to my shop and grab the FREE Indirect Measurement Lesson!}

More Middle School Math Resources to Try:

Similar Posts