Understanding the Distributive Property {FREE Lesson!}
I distinctly remember the week in 7th grade pre-algebra that was spent learning and (supposedly) understanding the distributive property. I remember this week so vividly because, for some reason, it made NO sense to me. None. At. All.
Eventually I understood what it meant, and how to use it and apply it in the wonderful world of Algebra and solving equations and working with expressions.
But I never forgot how confusing and nonsensical it seemed that first week. I don’t know if my teacher just could not explain it well or if I was having an “off” week or what the issue was, but once I became a math teacher myself, I was determined to teach this in a way that made sense. (Or at the very least, do my best to make it meaningful to students!)
*Please Note: Some of the links in this post are affiliate links. Read our full disclosure policy here.*
If you’re unfamiliar with this algebraic property, here’s a basic definition:
The distributive property says that when multiplying a sum or difference of terms, you can multiply each term or addend inside a parenthesis separately.
Now, I completely understand that that definition probably makes no sense. So I would never start a math lesson by telling students a wordy definition like that. How math is normally taught, however, is by showing some examples. Then, students are expected to repeat the process seen in the examples.
This didn’t work for me though. Again, looking at it now, it makes perfect sense, so I don’t know what the hang up was, but hearing a definition and seeing a bunch of examples did not make sense to me.
So what did I do differently? I tried to teach it through problem solving. I simply presented a problem to students and let them figure it out. Then I asked them probing questions to try and get them to explain what they did, whether with words, pictures or a math equation.
Only after solving some problems using the distributive property and discussing it did we move on to the more abstract algebra problems involving constants and variables.
The problem I gave went something like this:
Mrs. Jones is shopping for her twins birthday. She can spend any amount of money, but she has to buy exactly the same thing for each of them. Choose 3 gifts (and the prices) for her to purchase and determine the total cost.
There are several ways to solve this. First, you can add the cost of each of the 3 gifts together and then multiply by 2 (because there are 2 kids). For example, here’s what it would look like if the gifts cost $10, $25 and $40:
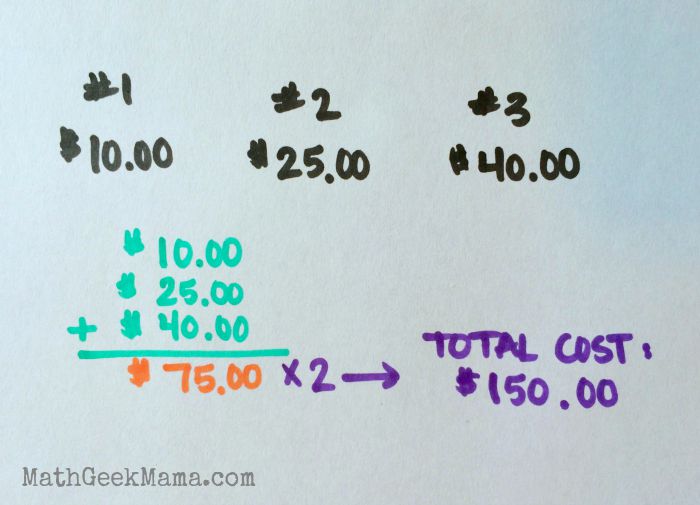
Or you can double the cost of each gift and then add the 3 gifts together.
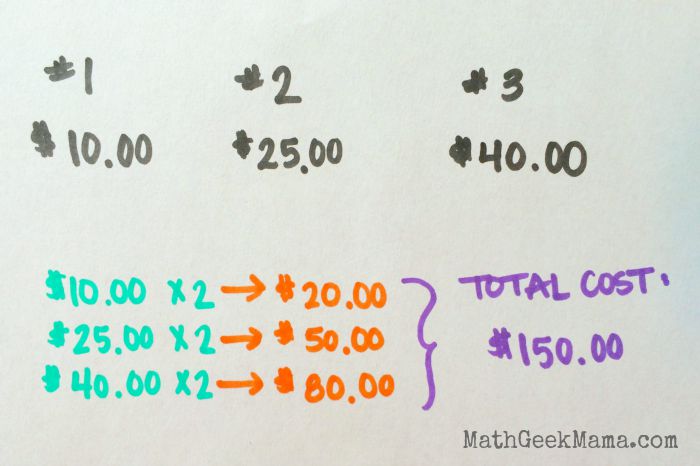
Thus, demonstrating the distributive property.
There are lots of things to discuss in this lesson, because students will solve it different ways, so let them discuss which is better or more efficient. Once you explain that they’ve used and demonstrated the distributive property, explain why it will be necessary in more challenging algebra problems–when you have unlike terms inside the parenthesis, you will not have the option to add first and then multiply, and so you “distribute.”
I’ve created a handy printable version of this lesson if you would like to use it with you pre-algebra or algebra students, which goes a little further and has some discussion questions (as well as an answer key).

{Click HERE to go to my shop and download the Distributive Property Lesson!}
I hope you find this useful in understanding the distributive property, and that you are able to help your students not only understand this algebraic property, but help them see yet another way they use algebra in their everyday life!
*Psst! If you found this lesson useful, be sure to check out my Algebra Essentials Resource Bundle! It includes this lesson, as well as another lesson which teaches the distributive property using the area model. Plus, SO much more! Click the graphic below to see everything that’s included.
If you enjoy this lesson, check out some of my other Algebra lessons:















4 Comments
Comments are closed.