How to Multiply Double Digits: Strategies & Game Ideas

As I wrapped up the school year with my third grader, we spent some dedicated time working on multiplication and trying to solidify the multiplication facts. But along with knowing what multiplication means and the importance of knowing the facts, I also wanted him to see how we can extend that knowledge to multiplying double digits and beyond. Although the sight of such large multiplication problems can be intimidating, it doesn’t have to be. Learn simple, yet powerful strategies for how to multiply double digits with ease. Then you can apply these ideas to even larger numbers and multiplying decimals.

*Please Note: This post includes affiliate links which support the work of this site. Read our full disclosure here.*

How to Multiply Double Digits: Use an Area Model

My favorite method for multiplying double digits is to draw an area model. This is helpful because it provides a visual of what the problem represents.

Plus, it can then be applied to more difficult problems later on, including multiplying polynomials in Algebra.

One way to think of multiplication is as the area of a rectangle. This means in any given multiplication problem, you can think of each factor as the length and width of a rectangle.

For example, let’s say we want to multiply 24 x 35. You can begin by drawing it as a rectangle with a width of 24 and length of 35.

At this point, you might be thinking, ‘Ok, that’s great. It’s a box now, but how in the world does that help me to solve it??’

Well, you can then break the box into sections that are easier to solve, as if you’re coloring in the area one small section at a time.

For example, I might separate the width into 20 and 4, then I might separate the 35 into 30 and 5, like this:

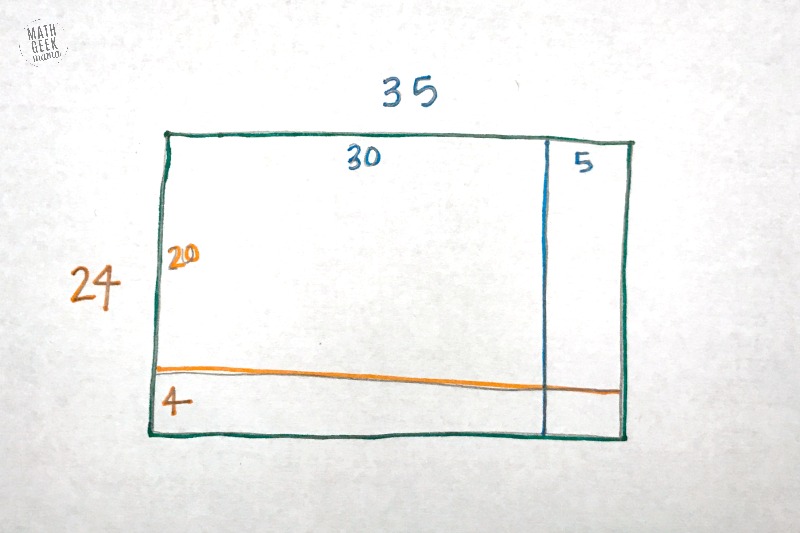
Now, I have smaller rectangular sections that I can multiply more easily. For instance, starting with the largest rectangle, we have 30 x 20 = 600:

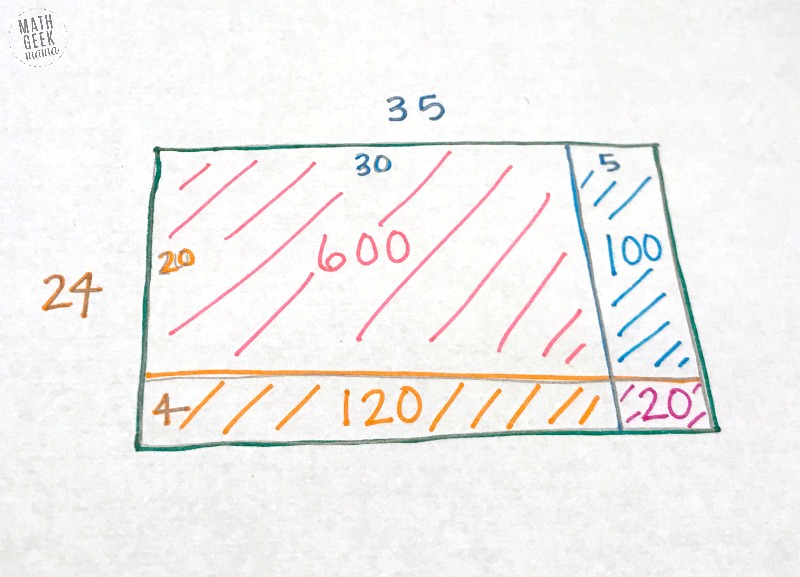
Then I can continue with the rest of the boxes:

30 x 4 = 120,

And 5 x 20 = 100,

And lastly, 5 x 4 = 20.

Now that I’ve found the area of each small section, I can add them together to find the total area (or the final solution to the original double digit multiplication problem: 24 x 35): 600 + 120 + 100 + 20 = 840

The Benefits of Using an Area Model

This visual is also helpful because it shows that multiplying larger numbers gives larger answers, which are evident in the picture (larger sections of the total rectangle).

The other great thing about this method is that kids can break apart the original rectangle in a million different ways. They can do what makes the most sense to them, or using whatever multiplication problems will be easiest for them to solve mentally.

There’s no ‘right’ or ‘wrong’ way. This gives kids freedom to make sense of the problem on their own and explore in their own way.

And if you see they tend to always choose the same strategy (such as separating the tens and ones), ask them to solve it a different way. This will force them to think about other ways to decompose the numbers that might work better or make solving the problem easier and more efficient.

Plus, it gives them additional practice with multiplication. 😉

For more on how to set up and solve using area models, see this article and grab a free template.

How to Multiply Double Digits: Use Place Value to Find Partial Products

Another helpful strategy that you may see kids use who have not been taught a formal algorithm is to use place value to break the problem apart and solve in pieces.

This is similar to using an area model, but it doesn’t include the visual.

This can be especially helpful when one of the numbers includes low, easy to multiply digits such as 2 or 3.

For example, let’s say you want to multiply 78 x 12.

You can then think of this instead as (78 x 10) + (78 x 2).

Multiplying by ten is easy, and this gives you 780.

Multiplying by 2 then is the same as doubling, so 78 x 2 = 156

You can then simply add the partial products together to get 780 + 156 = 936

Here’s another example: 48 x 14

In this example, we can think of this as (48 x 10) + (48 x 4)

The first part is easy, giving us 48 x 10 = 480

Multiplying 48 x 4 is not as easy to do mentally, but can then be broken down further as 48 x 2 and then x 2 again.

In other words, 48 x 2 = 96 and then 96 x 2 = 192

Then, again, we can add the partial products together to get 480 + 192 = 672

How to Multiply Double Digits: Using the Formal Algorithm

Lastly, once students have a solid understanding of what multiplication represents and feel confident breaking numbers apart and working through mental computation problems, you can introduce the formal algorithm.

I suggest sharing this last, because if kids have a solid understanding of how to work with and multiply double digit numbers already, the algorithm is not so scary.

If fact, it will likely make perfect sense for most kids. Because now, it doesn’t seem like random rules to follow and remember, but a handy dandy method of keeping track of what they were previously doing in their head.

So in case you’re unfamiliar, here’s a step by step example of multiplying double digits using the traditional algorithm. Let’s say now we want to multiply 34 x 62.

Step One: Line Up All the Digits

First, line up all of the numbers according to their place value.

Step Two: Multiply by the Ones Digit

Then begin by multiplying each digit of the top number by the ones digit (in this case, 2). In this example, we have 4 x 2 = 8 (write that in the ones place) and then 3 (which really means, 30) x 2 = 6 (which really means 60). You then write the 6 in the tens place.

Step Three: Add a Zero Place Holder

Then, place a zero under the ones column as you begin to multiply 34 by the 6 (which really means 60).

The reason for this zero is that you are not simply multiplying 34 by 6. You are multiplying 34 x 60. In other words, it is a multiple of ten, which is why we know we need to have that zero there.

Step Four: Multiply by the Tens Digit

Then you can multiply each digit by 6.

This gives 6 x 4 (which is really 60 x 4) = 24 (which is really, 240).

Because this actually represents 240, the 4 goes in the tens column in our solution, and then we ‘carry’ the 2, meaning we place it in the tens column at the top.

I usually record this as a ‘+2’ rather than simply a 2, because a lot of times kids forget whether they are supposed to add that or multiply it.

Then we multiply 3 x 6 = 18 and we add the 2, to equal 20 (which really represents 2000, because we’ve actually multiplied 30 x 60 and added another 200 to it).

Therefore, we end up with 2040 in the second row of our answer.

Step Five: Add the Two Answer Rows Together

Then, just as we did with our partial products, we add the two rows of solutions together to get 68 + 2040 = 2,108

When I teach my kids this procedure, I typically write out each step as a partial product as I work through the problem. This allows them to see where all the numbers are coming from, why we add the zero and why we add the answer rows together for the final answer.

Then, I let them practice, using whatever method or strategy is most effective and comfortable for them!

Multiplying Double Digits: Game Ideas

If you’re looking for some extra practice for your kids to multiply double digits, here are some games you might enjoy.

And be sure to check out this strategy for helping kids understand and see patterns as they multiply large numbers: How to Multiply Large Numbers Using Tables

I hope you found this helpful and maybe even learned some new ways of multiplying double digit numbers!