{FREE} Comparing Fractions Cut & Paste Practice with Visual Models

Giving five fractions to a child and saying, “Please put these in order from largest to smallest,” can be quite daunting. But there are so many strategies that they can use to make it a little easier. One way is to start by just comparing two fractions, and another way is to have the children order fraction models. These simple comparing fractions cut and paste worksheets use visual models rather than just fractions, helping to support kids’ developing understanding of fractions. And they are a great place to practice comparing fractions strategies that make ordering fractions easier.

*Please Note: This post includes affiliate links which help support the work of this site. Read our full disclosure here.*

This is a guest post from Rachel of You’ve Got This Math.

Get Started with the Comparing Fractions Worksheets:

The first two pages are very simple and focus on understanding the numerator and denominator.

The fractions on the first page are all unit fractions, meaning the numerator is equal to one.

With this page, you can help kids by asking what they would rather have: one piece of their favorite cake that has been divided into 3 equal parts, or one piece of their favorite cake that has been divided into 7 equal parts.

Of course, we would rather have the one that has been divided into three equal parts because we will get more. So 1/3 is greater than 1/7.

Next, all the denominators are the same, and this is easy for our children.

Most of our little ones they can easily see that the order from largest to smallest is 7/8, 6/8, 5/8, 4/8, 3/8 and then 2/8.

Comparing Fractions with Unlike Denominators:

The third page now has different denominators and numerators, but all the fractions are represented by circles.

Children can easily see which fractions are larger or smaller by looking at the models.

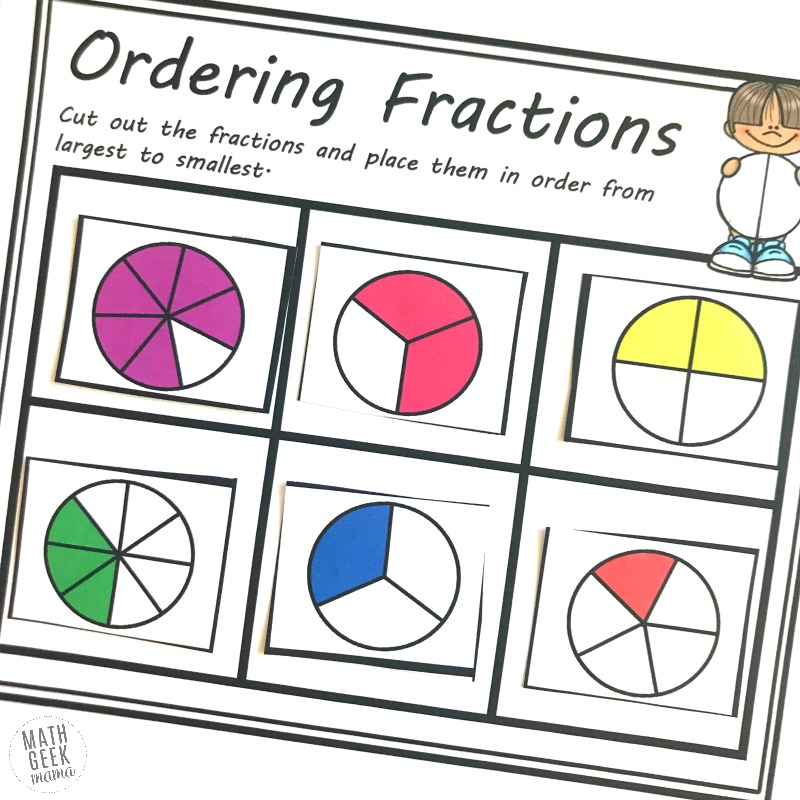
But to lay the foundations for the final two pages, you may want to encourage some strategy and reasoning. For example, have kids start by sorting them into two groups: those larger than 1/2 and those smaller.

1/3, 1/5, and 3/8 are all less than 1/2. We can easily see that 3/8 is largest, and we know from the previous sheets that 1/3 comes next, and then 1/5.

There is a model that equals 1/2.

Then all we have left is 2/3 and 5/6. It is pretty easy to see that 5/6 is larger than 2/3. But once again we can expand knowledge by having the children find equivalent fractions to prove this.

One way is to draw on the model to make the 2/3 model have six parts. Now we see that 2/3 is the same as 4/6.

Or we could do the work using a formal algorithm: 2/3 x 2/2 = 4/6.

With all that work done we now know the order from largest to smallest is 5/6, 2/3, 2/4, 3/8, 1/3 and finally 1/5.

Comparing & Ordering Fractions with Different Visual Models:

The fourth and fifth pages are the hardest, as there are many different shapes, different numerators, and different denominators.

The first step is to write the fractions next to the models. The models will help our visual learners visualize the fractions, but we can’t technically order the models because the pictures do not have equal pieces.

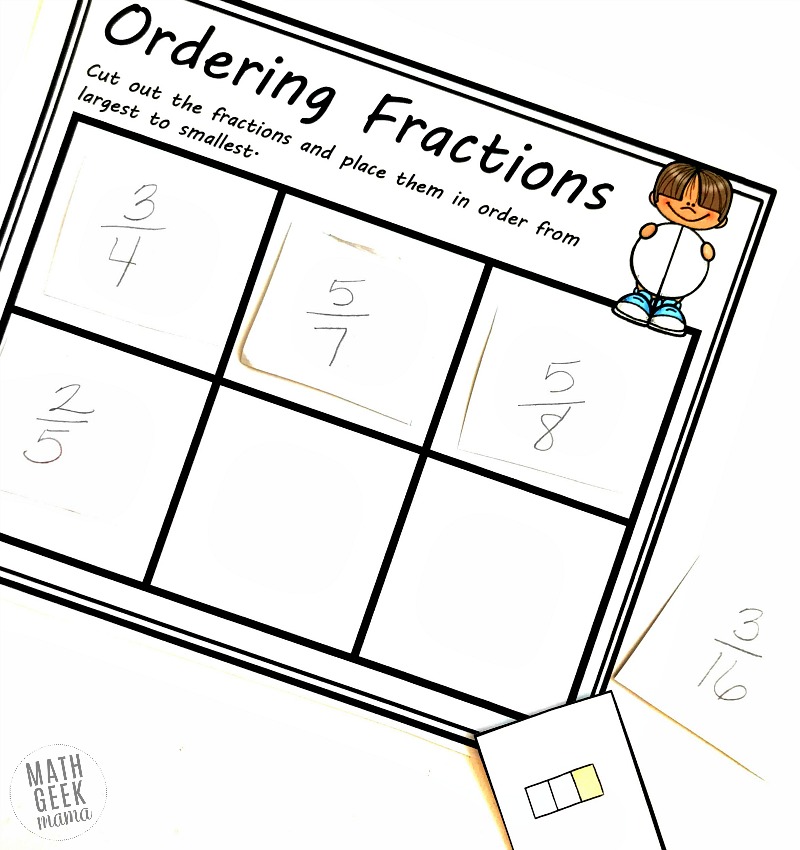
Next, we sort the fractions into two different piles. Those that are less than 1/2 and those that are greater than 1/2. This step helps narrow down where the fraction models will go.

Next, we look at one pile. In the pile that is less than 1/2, we have 1/3, 2/5, and 3/16. Just by looking we can see that 3/16ths is the smallest. Looking at 1/3 and 2/5 we might be able to tell that 1/3 is less, but let’s be sure by making equivalent fractions.

The least common denominator is 15, so we want to get both our fractions to a place where they have 15 as the denominator.

1/3 x 5/5 = 5/15

2/5 x 3/3 = 6/15

We were right 1/3 is smaller than 2/5!

Now we get to move into the pile that has fractions larger than 1/2. That pile consists of 5/7, 3/4, and 5/8. Just by looking, I can see that 5/8 is smaller than 3/4, and I know that 5/7 is larger than 5/8ths. (if the numerators are the same, the fraction with the smallest denominator is the largest fraction).

But I may not be able to tell with the 5/7 and 3/4. So let’s find the least common denominator and make equivalent fractions.

Twenty-eight is the least common denominator, so:

5/7 x 4/4 = 20/28

3/4 x 7/7 = 21/28

With this knowledge, we can place the last three in order from largest to smallest: 3/4, 5/7, 5/8

And that is how it is done. This provides some fun comparing fractions practice, while deepening an understanding of fractions, benchmark fractions and visualizing fractions.

Enjoy!

{Click HERE to go to my shop to grab this FREE set of Comparing Fractions Worksheets!}

Rachel is a homeschool mom to four little ones, ages 2 to 6. She is a former public elementary teacher, and has recently begun blogging at her page You’ve Got This. You can also find her on Facebook and Pinterest.