Exploring Patterns in Pascal’s Triangle {FREE Printables!}
When I taught Algebra, there were lots of ways I loved to explore patterns with kids and help them make the connection between a number pattern, a table, a graph and an equation. One way we did that was by looking at fractals. Another really fun way to explore, play with numbers and see patterns is in Pascal’s Triangle.

The pattern known as Pascal’s Triangle is constructed by starting with the number one at the “top” or the triangle, and then building rows below. The second row consists of a one and a one. Then, each subsequent row is formed by starting with one, and then adding the two numbers directly above. Therefore, row three consists of one, two, one. This pattern then continues as long as you like, as seen below.
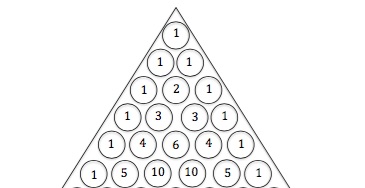
There are countless math ideas and patterns to explore in this cool triangle, depending on the age and ability of your students.
For young ones, simply seeing the sums and being able to complete the next row is great addition practice. They can also see the pattern of natural or counting numbers.
For older students, let them play around with it. See if they notice anything by adding each row. Or explore Pascal petals (a great way to practice prime factorization, and encourage kids to “prove” their observations).
Another fun idea might be to set a timer and see who can complete the most rows correctly in the set amount of time. This might be especially useful if your students need practice adding larger numbers.
For high school or statistics students, Pascal’s Triangle can help solve combination problems, which can often be very challenging. For example, say you have a class of 10 students and you want to know how many ways you can form a group of 6 for a math competition. Using Pascal’s Triangle, we can look at the 6th entry in row 10 to discover that the answer is 210. (This is assuming the first row is “row 0” and the first entry in each row is “entry 0.” So basically, you do not start counting with the “ones” in each row.)
High school students can also see that the numbers in Pascal’s Triangle give the coefficients in a binomial expansion.
For more information on the math and patterns found in Pascal’s Triangle, check out this Wikipedia article. And if you’ve already explored fractals, try this lesson to help students see the connection between Pascal’s Triangle and Sierpinski’s Triangle!
And if you’re looking for a fun introduction, I have a FREE Pascal’s Triangle lesson to share today!
The first page of this is a basic introduction to Pascal’s Triangle, which allows students to get familiar with it, and complete a couple more rows. Then there are some discussion questions for them to consider.

Then, because I think coloring is incredibly relaxing and calming, and creates amazingly beautiful math art, I’ve created some “Coloring Pascal’s Triangle” pages! These will help your kids visualize the patterns they learn and explore in the triangle. They start with very basic and simple ideas for young ones and then increase in difficulty.

But I would encourage you to also let your students create their own, based on their findings or favorite number pattern!
The coloring pages include a large, blank triangle, which requires students to fill it in with the correct numbers first, then proceed to color. This way they can become more familiar with the numbers and maybe see patterns they hadn’t noticed yet.

If your kids enjoy history, you may want to let them explore further by reading about the history behind it, and learning more about Blaise Pascal and his thoughts on the triangle. Or they may enjoy this mathematical tale by Theoni Pappas!

{Click HERE to go to my shop and download the Pascal’s Triangle Exploration and Coloring Pages!}
Whatever you decide, let your kids be creative and have fun playing with numbers and patterns!
Want more free resources and ideas from Math Geek Mama? Sign up for my FREE weekly newsletter and get access to exclusive freebies for subscribers!












This looks like fun. 🙂
Thank you for using color as an integral part of the mathematical thinking instead of decoration or “play” or “answer.” Congratulations. I’m interested in seeing more of what you do with color.
Thank you! Perfect – we need a blank template for Pascal’s Triangle, and the rest is very helpful. Out of interest, at what age are children generally introduced to this concept?
I’ll be looking at the rest of your site with interest!
Thanks Katherine! I think generally this is not something that is introduced until Middle school or High school, but my daughter (age 7) is capable of calculating several rows and seeing some of the patterns, which is why some of the lessons in this printable are easy enough for young kids! I hope you enjoy it! 🙂
We can use it in other ways like (12)whole square = 144 ,(12)raise to power cube =1728 etc
(a+b)whole square=a square+2(ab)+b square
Sir if we write (ab) whole square=a square 2ab b square
eg,(12)whole square = 1 square 2(1)(2) 2 square=1 4 4= 144
Similarly raise to power cube, raise to power 4 etc
Hi! How can i access the plan/ worksheets for the plan on Pascal’s Triangle??
Hi! If you go to the product page in my shop here: https://mathgeekmama.com/product/patterns-in-pascals-triangle/ you can “add to cart” and checkout. It’s free, and you will get a copy sent to your email. 🙂